Calculating the Area of a Circle Using Lines

The area of a circle has a well established and well known formula that is elementary when it comes to the field of geometry. However, almost no one who knows the formula knows how to prove it or show that it is true. There are more advanced ways to do it, but one way that is easy to visualize is to use lines that approximate the area. The key concept is that adding more and more lines makes the approximation more accurate, so if we add an infinite amount of lines, we arrive at the exact area.

Start with this drawing that uses just four lines, and notice how they create a roughly circular shape:

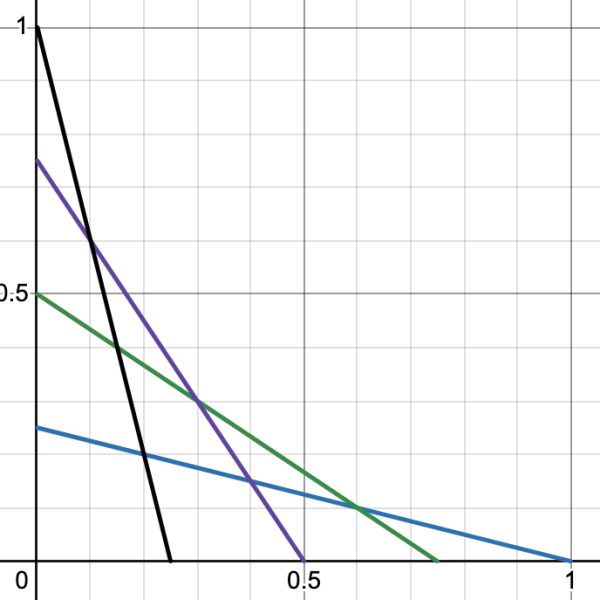
Adding more lines, it is clear that as the amount of lines increases the shape becomes more circular:

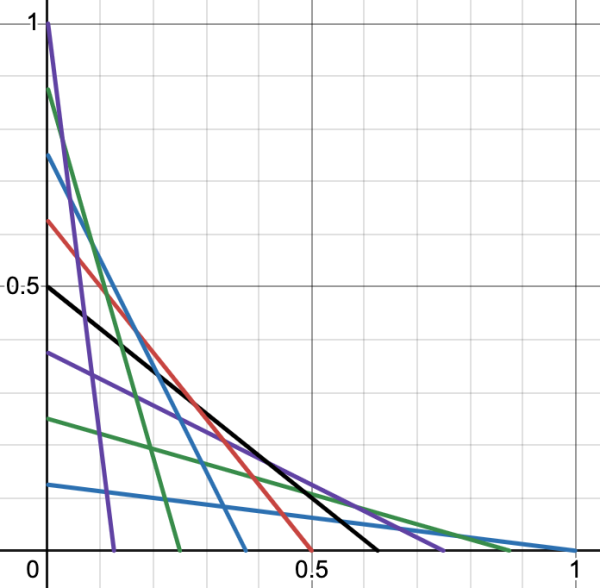
To approximate the area of a circle using this technique, we will subtract the area in the first quadrant below the circular border from the unit square in the first quadrant and multiply that value by four (since the difference of area will yield the area of a quarter circle).

The area below the border can be calculated using triangles formed by the lines:

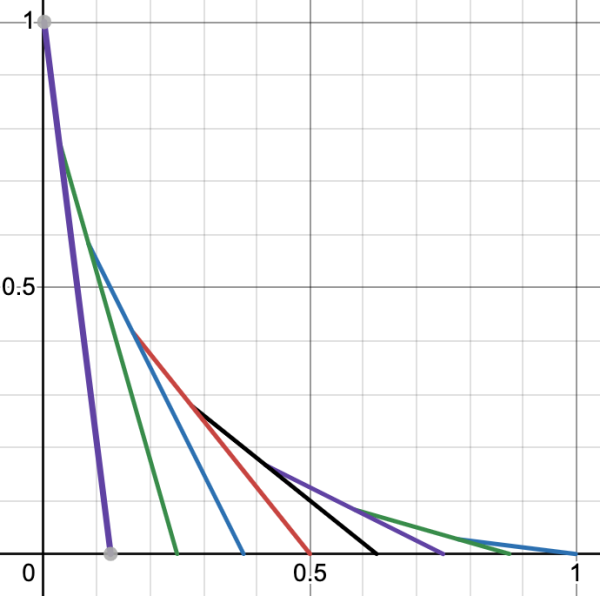
The base of each triangle is 1/n where n is the amount of lines, and the height of each triangle can be obtained by finding where adjacent lines intersect.

For the sake of being concise, the height of each triangle comes out to: ((n–j+1)/n)((-1/(j((n–j+2)/(j-1))-((n–j+1)/j)))+1). Where n is the number of lines, and j is the distance that the right border of the triangle is from the y axis times n.

Using the area of a triangle formula: T = (bh)/2 ; We have: T = ((n–j+1)/2n²)((-1/(j((n–j+2)/(j-1))-((n–j+1)/j)))+1).

Since the total area below the border and in the first quadrant is the sum of all the triangles, we have:

A = Σ{j=1,n}((n–j+1)/2n²)((-1/(j((n–j+2)/(j-1))-((n–j+1)/j)))+1)).

Therefore, the limit as the amount of lines approaches infinity can be written as:

lim{n→∞}(Σ{j=1,n}((n–j+1)/2n²)((-1/(j((n–j+2)/(j-1))-((n–j+1)/j)))+1)).

Using this to find the area of a circle, we will subtract the limit from the unit square in the first quadrant and multiply that value by four:

4(1 – lim{n→∞}(Σ{j=1,n}((n–j+1)/2n²)((-1/(j((n–j+2)/(j-1))-((n–j+1)/j)))+1))).

Comparing this to the simple formula for the area of a circle, we have the equation:

πr² = 4r²(1 – lim{n→∞}(Σ{j=1,n}((n–j+1)/2n²)((-1/(j((n–j+2)/(j-1))-((n–j+1)/j)))+1)) ; ∀r∈ℂ.