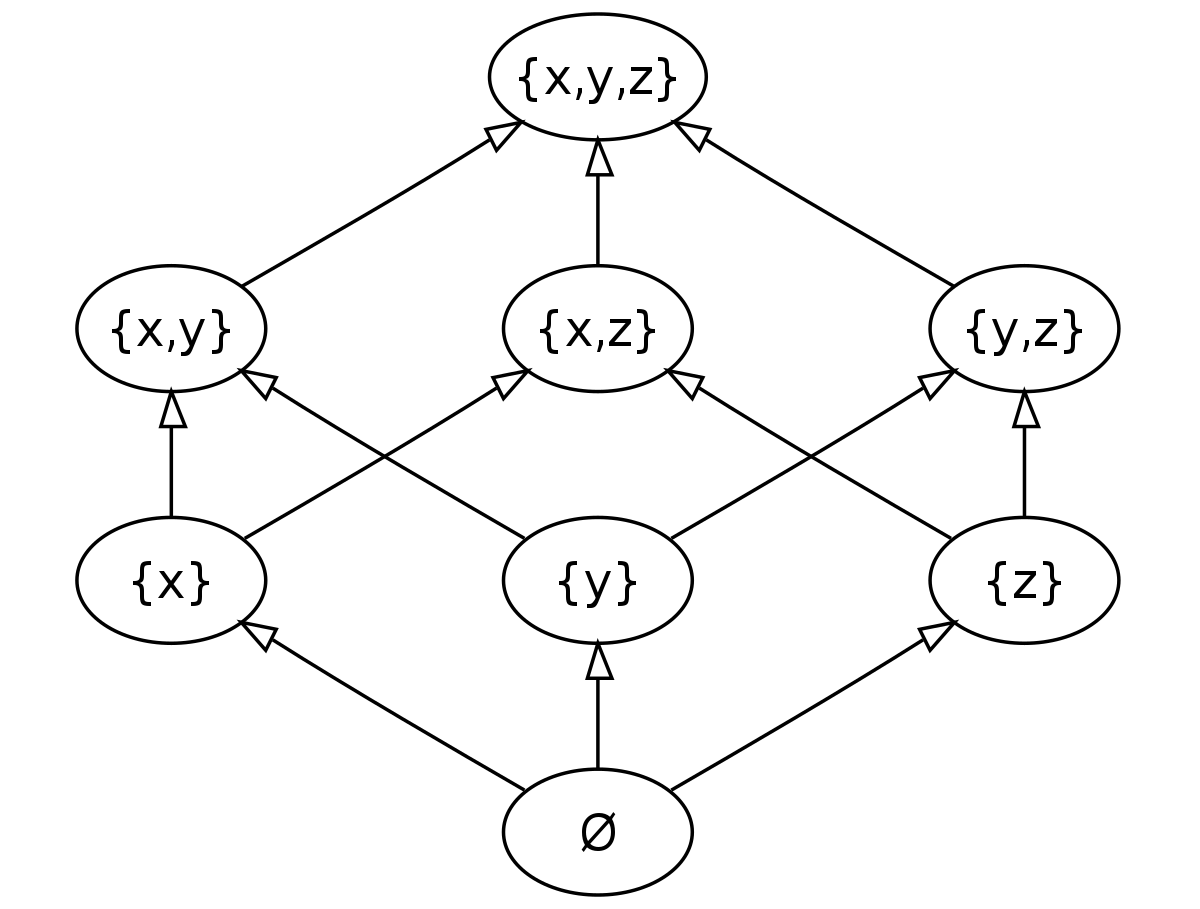
In set theory, a power set is the set of subsets of another set. For example, given a set A = {x,y,z}, its power set ℘(A) would be the set of all non ordered combinations of x, y, and z including the empty set and the set A itself. Therefore, ℘(A) = {(),(x),(y),(z),(x,y),(x,z),(y,z),(x,y,z)}.
The cardinality, or number of elements in a set, of any power set can be obtained using the distributive property of set theory. If we take the set A = {x,y,z} again for example, we can logically say that each element of ℘(A) either contains or does not contain each element of A. Now, this seems like an obvious statement, but we can use it to calculate the cardinality of the superset of A (which can also be written as |℘(A)|). The way we do this is by saying that ℘(A) is the same as all of the unique combinations of {(x∨¬x)∧(y∨¬y)∧(z∨¬z)}. The distributive property of set theory says that we can expand the previous expression into: {((x)∧(y∨¬y)∧(z∨¬z))∨((¬x)∧(y∨¬y)∧(z∨¬z)}. From this it is obvious that if we keep distributing we will arrive at ℘(A) and we can express |℘(A)| as 2|A|.
So, for a set S with n elements the cardinality of its super set is 2n. We can also calculate this value however using advanced algebra. Analyzing the composition of a superset ℘(S), we can see that its cardinality is the sum of its elements containing zero terms (the empty set), elements containing one term, elements containing two terms, etc. up to the element that contains n terms which is S itself. These values can be computed by (n!/(n-j)!j!) where n is still the cardinality of S and j is is the amount of terms in the elements that you are concerned with. Since we know that |℘(A)| equals the sum of the cardinalities of these specific elements from zero to n, we can express it as: ∑(n!/(n-j)!j!) over [j=0, j=n].
Therefore we arrive at the general conclusion that for all real whole numbers n: 2n = ∑(n!/(n-j)!j!) over [j=0, j=n].